原理
物質を構成する原子1つ1つに対して、古典力学におけるNewtonの運動方程式を解き、原子位置やエネルギーの時間変化を追跡する手法を分子動力学法(MD計算)と言う。古典的なMD計算では電子を考慮しないため、原子間に働く相互作用は、相互作用ポテンシャルエネルギーとして定義する関数に含める。この相互作用ポテンシャル関数は分子力場 (単に力場とも呼ばれる)として、対象系に応じて様々なポテンシャル関数が開発されている。MD計算では外場 (温度、電気、圧力など)を加えることが可能であり、時間変化を追跡することで、拡散係数や熱力学量など物性値に関する情報が得られる。また、上述した通り、古典的なMD計算では電子の運動を考慮しないため、系によっては計算精度が不十分な場合があるが、対象系の総てを第一原理的に取り扱う第一原理MD計算などにより、精度向上が取り組まれている。
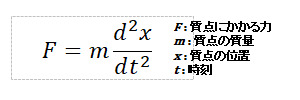
分子動力学計算より得られる情報
- 動径分布関数
- 自己拡散係数
- 各種熱力学量 (蒸気圧、密度分布、熱伝導率)
- 粘度
- 密度
- 弾性率
- 溶媒和自由エネルギー
- ガラス転移温度
- 線膨張率